Construções Históricas dos Radicais

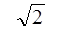
é possível sem calculadora?





A História da Matemática não traz apenas memórias sobre fatos particulares dessa ciência, oferece também, um recurso de reflexão importante à compreensão de conceitos dessa área do saber e mostra que, muitos dos conceitos usados, atualmente, tiveram um processo de construção e não nasceram como hoje os conhecemos.

Quando se estuda Matemática, pensa-se que tudo sempre se apresentou assim, como se “Gênios” tivessem definido esses conceitos e os demais deveriam desenvolver seus pensamentos a fim de entender o conteúdo ali analisado.

Sobre os radicais, a história da matemática nos mostra que o símbolo:






Onde n é um número natural maior que 2 e essa raiz terá as suas restrições, a partir de x, e do conjunto numérico que ele pertence, pois se n for 2, e x= -2, não faz sentindo extrairmos a raiz quadrada sugerida no conjunto dos números Reais.

Por volta do século IX e VI A.C, os Babilônios já apresentavam alguns registros de signos que, recentemente, chamamos de radicais. Nesse período, esses radicais eram representados por letras e números e não existia ainda um símbolo,como o citado acima, que resumisse a ideia do radical como temos hoje.

No contexto do ensino básico, têm-se algumas situações que se recorrem aos radicais para determinarmos a solução de tais problemas, como por exemplo, determinar a diagonal de um quadrado, de lado 1, e consequentemente, para essa situação tem-se que determinar o valor da raiz quadrada de 2, mas será que é impossível determinar esse valor desprovido de um instrumento moderno,como uma calculadora?

Essa resposta já era respondida bem antes da invenção dela como hoje se conhece, pois, Héron de Alexandria, - 10 d.C. a 75 d.C.- usou um método para determinar a raiz quadrada aproximada de um número n,natural, onde segundo ele é escrito como um produto de números positivos, como segue abaixo:







Escrevendo n,nos moldes exibidos nas fórmulas, I e II, já na Idade Média, a seguinte relação ,a seguir, também determina, com aproximação, o valor da raiz quadrada de n.

Assim, concepções históricas de conceitos dessa Ciência nos ajudam a conceber definições matemáticas, sem os tradicionais recursos tecnológicos que se tem, atualmente, e a conjectura de Héron, mostra-nos que exibir o valor aproximado de uma raiz quadrada nada mais é do que operar números racionais.

Desse modo, as operações com esses entes ficam, realmente, simples e divertida. Logo, basta munir-se de alguns exemplos e teremos boas aproximações para as raízes quadradas de Números Naturais.